Simulador EXANI-II Redacción indirecta

Simulador EXANI-II Redacción indirecta

Ago 11, 2022 | Simulador, Simulador E-II

Demuestra tus conocimientos

Cada que realices esta prueba diagnóstica se presentarán algunas preguntas diferentes. ¡Suerte!

/10
0 votos, 0 media
16553

Simulador EXANI-II. Redacción indirecta

Los nexos que unen dos proposiciones para formar una oración disyuntiva son o, u, o bien.

1 / 10

¿Qué tipo de relación se establece entre las proposiciones de la siguiente oración?
No sabía si se burlaban de él o lo compadecían. (Tolstoi)

La mayoría de los verbos terminados en –izar se escriben con z.

2 / 10

Identifica las letras faltantes de cada palabra.
Se debe penali__ar la ca__a de animales en peligro de extin__ión.

Observa que estas palabras se acentúan en la penúltima sílaba.

3 / 10

Selecciona la opción que corresponde a la forma de acentuación de las palabras que están en negritas:
Derribó el árbol, pero no escuchó ningún sonido.

La idea clave del refrán es que en ocasiones es muy difícil corregir a las personas.

4 / 10

¿Qué otro refrán transmite una idea semejante?
Árbol que crece torcido nunca su rama endereza.

Observa que se te solicita lo opuesto o antónimo de arduo, no un sinónimo.

5 / 10

Elije la opción cuyo significado sea opuesto a la palabra en negritas:
A menudo, el camino al éxito es arduo

Ayuda:

No te puedo ayudar

6 / 10

Elija las palabras que se escriben con diéresis.

  1. Nicarag_a
  2. Ung_ento
  3. Antig_edad
  4. G_ajiro

Piensa dónde leerías un texto similar.

7 / 10

Por sus características, que tipo de texto es el siguiente:
Comencé a escribir La ciudad y los perros en el otoño de 1958, en Madrid, en una tasca de Menéndez y Pelayo llamada El Jute, que miraba al parque del Retiro, y la terminé en el invierno de 1961, en una buhardilla de París. El manuscrito estuvo rodando como un alma en pena de editorial en editorial hasta llegar, gracias a mi amigo el hispanista francés Claude Couffon, a las manos barcelonesas de Carlos Barral, que dirigía Seix Barral.

Observa la concordancia de género y de número.

8 / 10

Selecciona el enunciado correctamente escrito.

Piensa que debe leerse en una revista especializada.

9 / 10

¿Qué texto reúne los atributos de un ensayo académico?

Observa que hay enunciados en que se prestan a confusión.

10 / 10

Identifique el enunciado cuya redacción sea la correcta.

Tu puntación es

La puntuación media es 60%

LinkedIn Facebook
0%

Por Wordpress Quiz plugin
Simulador EXANI-II Comprensión lectora

Simulador EXANI-II Comprensión lectora

Ago 11, 2022 | Simulador, Simulador E-II

Demuestra tus conocimientos

Cada que realices esta prueba diagnóstica se presentarán algunas preguntas diferentes. ¡Suerte!

/10
0 votos, 0 media
7047

1 / 10

[1] Gracias a un sofisticado sistema de navegación, [2] la mariposa monarca realiza cada año una travesía de más de 4 mil kilómetros desde Canadá hasta suelo mexicano. [3] Es un insecto de la orden de los lepidópteros y tiene una vida promedio de nueve meses. [4] Es la mariposa más famosa de México, Estados Unidos y Canadá.
Su viaje lo realiza a una altura de cien metros, a diferencia de otras mariposas que lo hacen casi a ras del suelo, aprovechando los vientos a esa altura para viajar más rápido.
Identifica el recurso utilizado para la redacción de las ideas del primer párrafo.

Lee con atención para encontrar la secuencia de los acontecimientos. Puedes numerar los acontecimientos en el examen para que te resulte más sencillo encontrar la respuesta correcta.

2 / 10

Ordena los acontecimientos cronológicamente.
Era ya de noche cuando más tranquilo repasó lo sucedido aquel día. Había corrido cuando menos tres kilómetros cuando escuchó a lo lejos el ulular de las patrullas, en ese momento supo que se encontraba a salvo; no como cuando escuchó el sonido seco de los primeros balazos. Aquella mañana, Roberto, sin saberlo, estacionó su auto justo enfrente de los asaltantes y de buen humor les preguntó si estaba prohibido estacionarse ahí; uno de ellos, desconcertado, dijo que no sabía. Momentos más tarde, lo volvió a encontrar cuando salía del banco a la carrera y con un arma en la mano; se miraron a los ojos y cuando observó que levantaba su arma hacia él echó a correr, escuchó un par de detonaciones y supo que su vida estaba en peligro.

  1. Supo que estaba a salvo
  2. Escuchó varios impactos de bala
  3. Corrió tres kilómetros
  4. Reconoció al asaltante
  5. Se estacionó frente a los asaltantes

Durante el relato el estado de ánimo de Roberto cambia, presta atención al texto.

3 / 10

Era ya de noche cuando más tranquilo repasó lo sucedido aquel día. Había corrido cuando menos tres kilómetros cuando escuchó a lo lejos el ulular de las patrullas, en ese momento supo que se encontraba a salvo; no como cuando escuchó el sonido seco de los primeros balazos. Aquella mañana, Roberto, sin saberlo, estacionó su auto justo enfrente de los asaltantes y de buen humor les preguntó si estaba prohibido estacionarse ahí; uno de ellos, desconcertado, dijo que no sabía. Momentos más tarde, lo volvió a encontrar cuando salía del banco a la carrera y con un arma en la mano; se miraron a los ojos y cuando observó que levantaba su arma hacia él echó a correr, escuchó un par de detonaciones y supo que su vida estaba en peligro.
¿Cuál era el estado de ánimo de Roberto cuando miró a los asaltantes por primera vez?

El título de un texto pretende dar una idea del contenido. De todos los títulos solo uno es el más adecuado

4 / 10

Fueron probablemente los griegos quienes primero reflexionaron sobre las propiedades de la magnetita, un mineral de hierro que incluso en estado natural posee una profunda atracción por el hierro. De hecho, Tales de Mileto alrededor del 600 a.C. ya habla del imán en forma detallada. Esto no excluye que éste ya se conociese en el resto del mundo. Por otra parte, Platón (428-348 a.C.) en su diálogo Ión hace decir a Sócrates que la magnetita no sólo atrae anillos de hierro, sino que les imparte un poder similar para atraer a otros anillos. De esta manera se forman cadenas de anillos colgados unos con respecto a otros. Estos son los llamados anillos de Samotracia, isla griega donde los mineros habían descubierto este fenómeno que en la actualidad llamamos magnetización por inducción.  (Tagüeña)
¿Qué título es el más adecuado para el texto anterior?

5 / 10

Lee el texto siguiente y contesta.
Acupuntura, opción para controlar el dolor
Existen muchos métodos que se han conservado desde la antigüedad y que han demostrado su efectividad. La acupuntura es uno de ellos y se ha utilizado recientemente para controlar el dolor, afirma un especialista del Instituto Politécnico Nacional. En un artículo publicado recientemente, el Dr. Carlos Chen asegura que mediante la acupuntura es factible controlar el dolor mediante este método en muy diversos casos, como quemaduras, operaciones sencillas y algunas neuropatías, gracias al profundo conocimiento que se ha alcanzado sobre las terminales nerviosas que es posible adormecer mediante la correcta aplicación de pequeñas agujas en algunas partes del cuerpo, y minimizar así la sensación de dolor. “La evidencia generada en los últimos tres lustros es sólida y ha demostrado capacidad para producir analgesia sin recurrir a fármacos”.
Sin embargo, esta técnica no funciona igual en todas las personas, hay quienes son más susceptibles a la acupuntura. En el informe se afirma que alrededor de la tercera parte de las personas puede beneficiarse con esta terapia, adicionalmente, una quinta parte podría hacerlo si practicara esta terapia, pero hay un porcentaje de personas que evidentemente requerirán fármacos.
Según el texto, la acupuntura puede emplearse como un método...

El tema central se refiere a la cuestión sobre la cual el autor comunica algo. Se debe leer con atención para poder interpretar correctamente lo que el autor pretende decir. 

6 / 10

Estudios demuestran que la lectura de ficción puede ayudar a mejorar las tendencias empáticas en las personas tanto que el cerebro usa las mismas regiones cuando se lee una historia que cuando se actúa por empatía. Leer ficción literaria que incite una gran simpatía hacia los personajes es una medida muy adecuada para poner en práctica esta teoría de la mente relativa a la función de la lectura en el desarrollo de las personas.
¿Cuál es la idea principal del texto?

Para responder necesitas conocer las sumas de ventas individuales y por equipos, así que debes complementar la tabla.
Lee con atención y descarta las opciones que evidentemente son equivocadas.

7 / 10

Lee el texto y contesta la pregunta.
Cuatro estudiantes se encargaron de vender boletos para una rifa de fin de año. Se organizaron en equipos, por lo que María y Pedro integraron el equipo A y Susana y Juan, el B. El equipo con mayores ventas obtendría dos boletos como premio; quien individualmente vendiera más, obtendría un boleto adicional y se obsequiaría un boleto extra a los hombres o a las mujeres, según sus ventas.
Las ventas fueron las siguientes.

Lunes Martes Miércoles Jueves Viernes
María 350 120 240 340 220
Susana 200 225 200 125 150
Pedro 135 145 250 130 200
Juan 200 250 210 220 350
Total 885 740 900 815 920

¿Cuál afirmación es correcta?

Desde el primer párrafo se indica que el advenimiento de la era espacial ha rebolucionado las ciencias; los siguientes párrafos hablan del desarrollo de la exploración del espacio

8 / 10

[1] Los descubrimientos producidos en la era espacial revolucionaron tanto a las ciencias básicas como a las aplicadas y a las sociales. Así, se abrieron nuevos rumbos para la geofísica, la astronomía, la física del sistema solar, la climatología y las comunicaciones; e incluso se abrieron nuevas disciplinas satelitarias como la cometología, la telecomunicación y el derecho espacial, entre otras.
[2] Antes de la era espacial, el hombre, para la exploración de los planetas, sólo contaba con telescopios ópticos y de radiofrecuencia. Estos aparatos le proporcionaban una información no nítida debido, en parte, a las distancias de centenas y hasta miles de millones de kilómetros existentes entre los planetas observados y la Tierra.
[3] Con el advenimiento de la era espacial el hombre logró enviar al espacio múltiples naves dotadas de instrumentos para realizar misiones de exploración de los planetas del sistema solar. Tanto las naves como los instrumentos fueron totalmente automatizados, sin presencia ni participación de astronautas.
[4] La exploración de los planetas se realizó con diversos métodos. Para ello, las naves algunas veces solamente pasaban en la cercanía de los planetas; y algunas otras, las naves tenían una permanencia relativamente larga en órbita planetaria.

Ruth Gall

¿Qué conclusión se desprende del texto?

9 / 10

Era una noche espléndida como sólo en ciertos lugares del trópico, y específicamente en Cuba, suelen observarse. De la tierra y del mar brotaba una pálida fosforescencia. Cada árbol parecía sobrecogerse sobre su propia aureola. El cielo, en aquel pequeño pueblo donde aún se desconocía la electricidad, resplandecía con la potencia de un insólito candelabro. [1] El pueblo (ahora lo llaman ciudad) era minúsculo, absolutamente provinciano y aburrido, [2] tan diferente de la calle del Obispo, siempre llena de pregones, carruajes, olores, mujeres, caballos y hombres. (Reinaldo Arenas)
¿Qué relación mantienen los enunciados 1 y 2?

La idea principal de un texto en generalmente está relacionada con la intención del autor.

10 / 10

[1] Los descubrimientos producidos en la era espacial revolucionaron tanto a las ciencias básicas como a las aplicadas y a las sociales. Así, se abrieron nuevos rumbos para la geofísica, la astronomía, la física del sistema solar, la climatología y las comunicaciones; e incluso se abrieron nuevas disciplinas satelitarias como la cometología, la telecomunicación y el derecho espacial, entre otras.
[2] Antes de la era espacial, el hombre, para la exploración de los planetas, sólo contaba con telescopios ópticos y de radiofrecuencia. Estos aparatos le proporcionaban una información no nítida debido, en parte, a las distancias de centenas y hasta miles de millones de kilómetros existentes entre los planetas observados y la Tierra.
[3] Con el advenimiento de la era espacial el hombre logró enviar al espacio múltiples naves dotadas de instrumentos para realizar misiones de exploración de los planetas del sistema solar. Tanto las naves como los instrumentos fueron totalmente automatizados, sin presencia ni participación de astronautas.
[4] La exploración de los planetas se realizó con diversos métodos. Para ello, las naves algunas veces solamente pasaban en la cercanía de los planetas; y algunas otras, las naves tenían una permanencia relativamente larga en órbita planetaria.

Ruth Gall

¿Cuál es la idea principal del texto?

Tu puntación es

La puntuación media es 59%

LinkedIn Facebook
0%

Por Wordpress Quiz plugin

Simulador EXANI-II. Módulo Cálculo diferencial e integral

Simulador EXANI-II. Módulo Cálculo diferencial e integral

Ago 11, 2022 | EXANI-II, Simulador E-II

Demuestra tus conocimientos

Cada que realices esta prueba diagnóstica se presentarán algunas preguntas diferentes. ¡Suerte!

Primer examen de Cálculo diferencial e integral

0 votos, 0 media
1490

Móduo de Cálculo diferencial e integral

Aplica una de las reglas básicas de derivación, según corresponda:
(k es una constante, u y v son funciones de x)
1) D? [ k ] = 0
2) D? [ x ] = 1
3) D? [ x n ] = n x n - 1
4) D? [ k u ] = k D? [ u ]
5) D? [ u ± v ] = D? [ u ] ± D? [ v ]
6) D? [ u · v ] = D? [ u ] · v + u · D? [ v ]
7) D? [ u / v ] = ( D? [ u ] · v - u · D? [ v ] ) / v2

1 / 10

Calcula la derivada f'(x) de la siguiente función:
f(x) = -17

Aplica las reglas básicas de derivación.

2 / 10

Calcula la derivada f'(x) de la siguiente función:

f(x)=5x3

Aplica las reglas básicas de derivación, según corresponda:

1) Dx [ k ] = 0 2) Dx [ x ] = 1 3) Dx [ xn ] = n xn-1 4) Dx [ k u ] = k Dx [ u ] 5) Dx [ u ± v ] = Dx [ u ] ± Dx [ v ] 6) Dx [ u · v ] = Dx [ u ] · v + u · Dx [ v ] 7) Dx [ uv ] = ( Dx [ u ] · v - u · Dx [ v ] )v2

Donde: k es una constante, u y v son funciones de x.

3 / 10

Calcula la derivada f'(x) de la siguiente función:

f(x) = -8x8 + 6x5 - 3x3 + 5x - 45

Recuerda que

∫ sec2 u du = tan u

4 / 10

Encuentra la integral de

∫ 16x7 sec2( x8) dx

5 / 10

Encuentra el área comprendida entre:

f(x) = x2 - 3

g(x) = 4 - x2


En el rango [0, 1.87], observa que es una suma de áreas.

Utiliza

[1,n] ∑ (cn + n) = [1,n] ∑ cn + [1,n] ∑ n

6 / 10

Encuentra la suma S = [1,36]:

∑ ( 50n + n )

7 / 10

Partiendo de la función:

f(x) = 2x3 + 14

Cuál es el valor para:

limx→2?f(x)

 

Utiliza la regla de la cadena para derivación de funciones exponenciales y logarítmicas:

1) Dx [ au] = ln a · au · Dx [ u ] 2) Dx [eu] = eu · Dx [ u ] 3) Dx [ ln u ] = Dx[ u ]u

Donde a es una constante y u es función de x

8 / 10

Encuentra la derivada f'(x) de la siguiente función:

f(x) = e( -8x - 25 )

Utiliza la regla de la cadena para derivadas de funciones compuestas:

Dx [ u(v) ] = u'(v) · v'

Recuerda las regla especial de derivación de raíces:

Dx [ x ] = 12x

Donde u y v son funciones de x

Dx [ x ] = 12x

 

9 / 10

Encuentra la derivada f'(x) de la siguiente función:

f(x) =
(-3x3 - 6)

Donde:

-3x3 - 6 > 0

Recuerda que

∫u du =un+1n+1

10 / 10

Sea:

f'(x) =10x4dx

Encuentra f(x), donde:

f(2) = 70

Tu puntación es

La puntuación media es 51%

LinkedIn Facebook
0%

Por Wordpress Quiz plugin

Cálculo diferencial e integral

Ago 10, 2022 | EXANI-II, Teoría EXANI-II

Para las ingenierías, la arquitectura y las ciencias exactas se utiliza este módulo de Cálculo diferencia e integral, que con 24 preguntas evalúa el dominio de este conocimiento especializado de las matemáticas.

Busca saber si los aspirantes a la universidad conocen el teorema fundamental del Cálculo y los conceptos de límite de funciones, los procesos de derivación e integración, la derivada y la integral, con los cuales es posible solucionar diversos problemas, tanto teóricos, como de aplicación a situaciones o fenómenos reales.

Los siguientes son los temas que de acuerdo con la guía oficial serán evaluados.  

Para las ingenierías, la arquitectura y las ciencias exactas se utiliza este módulo de Cálculo diferencia e integral, que con 24 preguntas evalúa el dominio de este conocimiento especializado de las matemáticas.

Busca saber si los aspirantes a la universidad conocen el teorema fundamental del Cálculo y los conceptos de límite de funciones, los procesos de derivación e integración, la derivada y la integral, con los cuales es posible solucionar diversos problemas, tanto teóricos, como de aplicación a situaciones o fenómenos reales.

Los siguientes son los temas que de acuerdo con la guía oficial serán evaluados.  

Cálculo diferencial
  • Límites
  • La derivada
  • Aplicaciones de la derivada
Cálculo Integral
  • Límites
  • Métodos de integración
  • Aplicaciones de la integral definida

El siguiente examen te puede orientar sobre los temas en los que debes prestar marpy atención.

¡Suerte! 

0 votos, 0 media
1490

Móduo de Cálculo diferencial e integral

Utiliza la regla de la cadena para derivadas de funciones compuestas:

Dx [ u(v) ] = u'(v) · v'

Recuerda las regla especial de derivación de raíces:

Dx [ x ] = 12x

Donde u y v son funciones de x

Dx [ x ] = 12x

 

1 / 10

Encuentra la derivada f'(x) de la siguiente función:

f(x) =
(-3x3 - 6)

Donde:

-3x3 - 6 > 0

Utiliza

[1,n] ∑ (cn + n) = [1,n] ∑ cn + [1,n] ∑ n

2 / 10

Encuentra la suma S = [1,36]:

∑ ( 50n + n )

Recuerda que

∫ sec2 u du = tan u

3 / 10

Encuentra la integral de

∫ 16x7 sec2( x8) dx

4 / 10

Encuentra el área comprendida entre:

f(x) = x2 - 3

g(x) = 4 - x2


En el rango [0, 1.87], observa que es una suma de áreas.

h = 0.5gt2, donde g = 9.81 m/s2

5 / 10

Un niño arroja una piedra en un acantilado. Tras esperar 14.25 segundos, escucha que la piedra toca el fondo. Determina la altura (en metros).

6 / 10

Partiendo de la función:

f(x) = 2x3 + 14

Cuál es el valor para:

limx→2?f(x)

 

El cálculo de límites por métodos algebraicos se basa en la aplicación de Teoremas o Propiedades de Límites

7 / 10

Calcula el siguiente límite:

limx→5?(x -5) (x +5)(x - 5)

Recuerda que:

∫udu =un+1n+1

8 / 10

Encuentra la integral "I" de:

∫-63x8dx

Aplica las reglas básicas de derivación.

9 / 10

Calcula la derivada f'(x) de la siguiente función:

f(x)=-9x-3

Aplica las reglas básicas de derivación.

10 / 10

Calcula la derivada f'(x) de la siguiente función:

f(x)=5x3

Tu puntación es

La puntuación media es 51%

LinkedIn Facebook
0%

Por Wordpress Quiz plugin

Pensamiento matemático

Ago 10, 2022 | EXANI-II, Teoría EXANI-II

En la guía de estudios oficial se da una definición de pensamiento matemático, se incluye una tabla con la estructura de esa sección del examen, un ejemplo de reactivo y una bibliografía, pero no nos dice qué temas estudiar… No te preocupes, te daremos pistas sobre los contenidos que debes estudiar para obtener una puntuación alta.

En pocas palabras, las preguntas de esta sección del examen buscan conocer tu habilidad para comprender, analizar y aplicar tus conocimientos para solucionar problemas en los que intervienen las matemáticas. Si a la tabla de la guía le añadimos contenidos, puede representarse así:

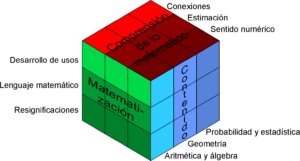
Por la forma en que están diseñadas, las preguntas te permiten utilizar gran variedad de estrategias para resolverlas, pues lo importante es encontrar las soluciones sin importar los procedimientos o reglas que utilizaste. Puede emplearse alguna técnica aprendida en la escuela, como fórmulas y ecuaciones, pero también pueden contestarse con el auxilio de dibujos o tablas, resolviendo problemas similares, por aproximación, por acierto y error, incluso por simple sentido común. Deducir y utilizar modelos de solución, utilizar las propiedades de los números, conocer los algoritmos o simplemente someter a prueba cada respuesta son recursos válidos al contestar la prueba.

En resumen, tendrás que estudiar aritmética, álgebra, geometría y probabilidad y estadística. El tema de cálculo diferencial y otras matemáticas más avanzadas se preguntan en los módulos disciplinarios.

 El siguiente es un examen de repaso. Practica varias veces con él, pues en cada ocasión te presentará algunas preguntas diferentes.

Te aconsejamos que midas el tiempo que te toma contestar cada pregunta. Es un dato que será importante para cuando presentes el examen real.  

/10
0 votos, 0 media
8424

Simulador EXANI-II. Pensamiento matemático

Suma la medida de la línea y el espacio entre líneas; convierte los kilómetros a metros y procede a realizar la división.

1 / 10

La distancia de la Ciudad de México a Acapulco es de 395 kilómetros. Si en esa carretera las líneas que separan los carriles miden 5 metros y la separación entre ellas es de 6 metros, ¿cuántas líneas tiene pintadas ese tramo carretero?

La fórmula del producto de dos binomios conjugados es
a2 - b2 = (a + b) ( a - b).

2 / 10

Factoriza la expresión 
c22 - v28    

3 / 10

Elije la figura que sigue para continuar la sucesión:

Si utilizas el método de sustitución debes despejar una incógnita en una ecuación y sustituirla en la otra ecuación.
Podrías empezar así:
Tenemos el conjunto de ecuaciones

V1L1 + L2

L1 + V3L2
 = R3
= R4

Despejamos c en la segunda ecuación

L1 + V3L2

L1
 = R4
= R4 - V3L2

Ahora sustituye el valor de c en la otra ecuación.

4 / 10

Juan compró 5 kgs de jamón (c) y un kilogramo de queso (x) por 320 pesos. Al día siguiente compró un kilogramo de jamón y 3 kilogramos de queso por 260 pesos. ¿Si los precios por kilogramo se mantuvieron fijos en las dos compras, cuánto cuesta el kilogramo de jamón y cuánto el de queso?

Utiliza la fórmula de desviación estándar

2 = (x2 p) - 2

5 / 10

El equipo de futbol de la preparatoria ha registrado en la temporada la siguiente distribución de goles anotados en un partido:

 

Goles Frecuencia p(x) x2 x2 p
0 14% 0.14 0 0
1 22% 0.22 1 0.22
2 9% 0.09 4 0.36
3 7% 0.07 9 0.63
4 5% 0.05 16 0.8
5 19% 0.19 25 4.75
6 24% 0.24 36 8.64

Si su esperanza matematica es 1.76, encuentre la desviación estandar "d".

En un producto de potencias, éstas se suman:

am · an = am+n

6 / 10

Simplifica la expresión

s-3 · s7

Calcula el área del cuadrado y del semicírculo por separado.
Recuerda que la fórmula para determinar el área de un cuadrado es:

 

A = L2

Un semicírculo es la mitad de un círculo, y por lo tanto su área es:

 

S = p r22

 

7 / 10

Determine la superficie en azul que se debe pintar. Se trata de una pared cuadrada en el que hay una ventana en forma de semicírculo cuyo diámetro es igual al largo del cuadrado exterior. El valor de x es de 5 m.

La fórmula del producto notable cuadrado de un binomio de resta es:

a2 - 2ab + b2
(Escribe la respuesta de forma ordenada)

8 / 10

Desarrolla la expresión

(5b - 6x3)2

Utiliza permutaciones o el principio de la multiplicación

9 / 10

En un concurso hay 6 candidatos a tres premios.
¿De cuántas formas se pueden ocupar los tres primeros lugares entre los  6 candidatos?

Podrías plantear el problema como
x + (x + 1) + (x+2) = 258

10 / 10

La suma de tres números consecutivos es 258 ¿de qué números se trata?

Tu puntación es

La puntuación media es 55%

LinkedIn Facebook
0%

Por Wordpress Quiz plugin